Les sondages sont-ils faux ?

Avec un tel titre, on pense tout de suite aux sondages d’opinion. Or il existe des tas de sondages comme par exemple le fait de tester des pièces à la sortie d’une chaîne de fabrication ou de vérifier certains justificatifs dans une comptabilité. L’objet de cet article vise bien l’ensemble de ces sondages, y compris les sondages électoraux.

A chaque élection, le débat sur la fiabilité des sondages revient d’ailleurs sur le devant de la scène mais la justification mathématique n’est jamais (à notre connaissance) remise en cause.

Disons-le tout de suite, si vous interrogez 1000 personnes et que vous notez soigneusement leurs réponses, disons par exemple que 550 ont répondu voter pour le candidat A, que vous publiez les chiffres que vous obtenez, autrement dit que vous affirmez avoir 55% de personnes qui ont indiqué voter pour A sur les 1000 personnes de votre échantillon, il serait malhonnête d’affirmer que votre sondage est faux.

Ce qui pourrait être faux, c’est ce que vous ferez du résultat de votre enquête, comme par exemple affirmer que 55% des électeurs de toute la population vont voter pour le candidat A parce que vous avez obtenu 55% de personnes disant voter pour A dans votre échantillon de 1000 sondés.

En principe, ce qui est affirmé est plus nuancé, c’est un intervalle de confiance, autrement dit une probabilité. Dans notre exemple, il pourrait être dit qu’il y a 95% de chances qu’il y ait dans la population totale entre 45% et 65% de personnes votant pour A. Ces chiffres sont supposés avoir été obtenus par un calcul mathématique et portent donc avec eux une image de sérieux et de légitimité qui est attachée à tout ce que produit la reine des sciences que sont les mathématiques.

Or, ces calculs sont faux.

On connaissait déjà les biais des sondages d’opinion, comme le fait que les sondés ne sont pas tirés au hasard (ce qui est un préalable obligatoire pour la justification mathématique), que les gens interrogés ne disent pas la vérité, etc. On ajoute maintenant dans ce texte un autre biais: celui du traitement mathématique non légitime. En fait, on va le voir, il est difficile de parler simplement de biais alors que c’est toute la démarche qui est ici mise en cause.

La situation

Illustrons le problème par un exemple moins scabreux que les opinions des êtres humains. Imaginons que vous ayez un jeu classique de 52 cartes. Il contient donc 13 cartes de chaque « couleur »: trèfle, pique, cœur et carreau. Les mathématiques vous disent que si vous tirez au hasard 5 cartes, vous pouvez calculer la probabilité d’obtenir exactement 2 trèfles (et donc 3 autres cartes qui seront d’une autre couleur). Ce calcul n’est pas contesté dans la communauté scientifique.

Mais ce qui se passe dans cette situation, c’est que vous connaissez parfaitement la composition de la population totale de vos 52 cartes et que vous calculez la probabilité d’avoir tel ou tel échantillon. Le calcul vous dira par exemple que vous avez 77% de chances d’avoir un tirage contenant entre 1 et 4 trèfles. Vous pouvez d’ailleurs vérifier que cela marche en effectuant des tirages répétés et même très nombreux. Vous constaterez alors que vous tendez progressivement vers 77% de tirages qui ont entre 1 et 4 trèfles.

Cette démarche n’est pas remise en cause : connaissant la population, vous calculez les probabilités d’avoir des échantillons dans un certain intervalle de confiance. Pas de problème.

Mais ce qui est fait avec les sondages, c’est exactement l’inverse.

Cela correspondrait à tirer 5 cartes dans un jeu de 52 cartes dont on ne connaîtrait absolument pas la composition.

Imaginez que quelqu’un ait constitué un jeu de 52 cartes avec toutes les cartes qu’il désire. Par exemple, il a rempli le jeu uniquement avec des trèfles. Ou bien il n’en a mis aucun. Ou encore il en a mis seulement 1 ou 2. Donc au final n’importe quel nombre compris entre 0 et 52. Et bien entendu, vous pouvez tirer 5 cartes de ce jeu mais rien ne vous est dit sur la composition du jeu lui-même.

Si vous regardez cet échantillon de 5 cartes tirées au hasard parmi ces 52 cartes et que vous observez par exemple qu’il y a deux trèfles, que pouvez-vous en déduire ?

La réponse est : que le jeu contenait au moins 2 trèfles et au maximum 49 puisque vous avez 3 non-trèfles. Rien d’autre.

Pourtant, avec vos 2 trèfles, vous pouvez affirmer que vous avez, dans l’échantillon, 40% de trèfles (2/5 = 40%). Vous avez aussi parfaitement le droit de vous demander quelle est la probabilité d’obtenir cet échantillon si votre population possédait 40% de trèfles. Et vous pouvez surtout calculer cette probabilité dans le cadre de cette hypothèse. Mais vous ne pourrez absolument rien déduire sur la valeur de cette hypothèse.

Dans un premier temps, nous allons démontrer ce que nous disons. Nous devrons ensuite expliquer les erreurs commises, c’est-à-dire le « comment » cette erreur est insérée dans le discours répandu parmi les utilisateurs des sondages. Enfin, et il ne s’agira dans ce cas que de spéculation même si elle est argumentée, il faudra bien tenter de répondre à « pourquoi », c’est-à-dire essayer de comprendre comment cette erreur a pu être commise et traverser des décennies voire des siècles sans être relevée.

1 – la démonstration

Elle est en fait très simple. Elle découle du principe des informations disponibles. Celles-ci ne peuvent en aucun cas « générer » des informations que l’on n’avait pas au départ. En logique, la déduction, ou plus exactement l’implication, consiste à présenter une partie réduite de l’information initiale. Eventuellement, cette information peut ne pas être réduite mais dans ce cas, il ne s’agit que de la même information sous une présentation différente. Quoi qu’il en soit, en aucun cas cette information ne peut être augmentée.

Exemple 1 : Considérons une information sur les livres d’une librairie donnée.

L’information initiale est donnée par : « tous les livres de cette librairie sont en français »;

la même information (donc 100% de l’information initiale) : « Aucun des livres de cette librairie n’est écrit dans une langue étrangère »;

information (réduite) déduite de l’information initiale : « Les livres de la vitrine de cette librairie sont en français ». On perd ici l’information sur les autres livres.

Exemple 2 : Soit un nombre réel x.

Information initiale : « 2x + 3 > 3 »;

la même information (donc 100% de l’information initiale) : « x > 0 »;

information (réduite) déduite de l’information intiale : « x > -1 » . Ici on perd l’information que x ne peut être compris entre -1 et 0.

Ainsi, appelons A un ensemble d’informations. Si vous savez que A est vrai, alors toutes les informations de A sont vraies et c’est donc aussi le cas de toutes les informations d’une partie B de cet ensemble A. On a donc A => B. Et si vous considérez un ensemble C d’informations qui ne sont pas dans A, vous ne pourrez rien déduite sur la véracité de celles-ci. Certes, vous pourrez collecter ailleurs des informations sur C mais vous ne pourrez pas les déduire de celles de A.

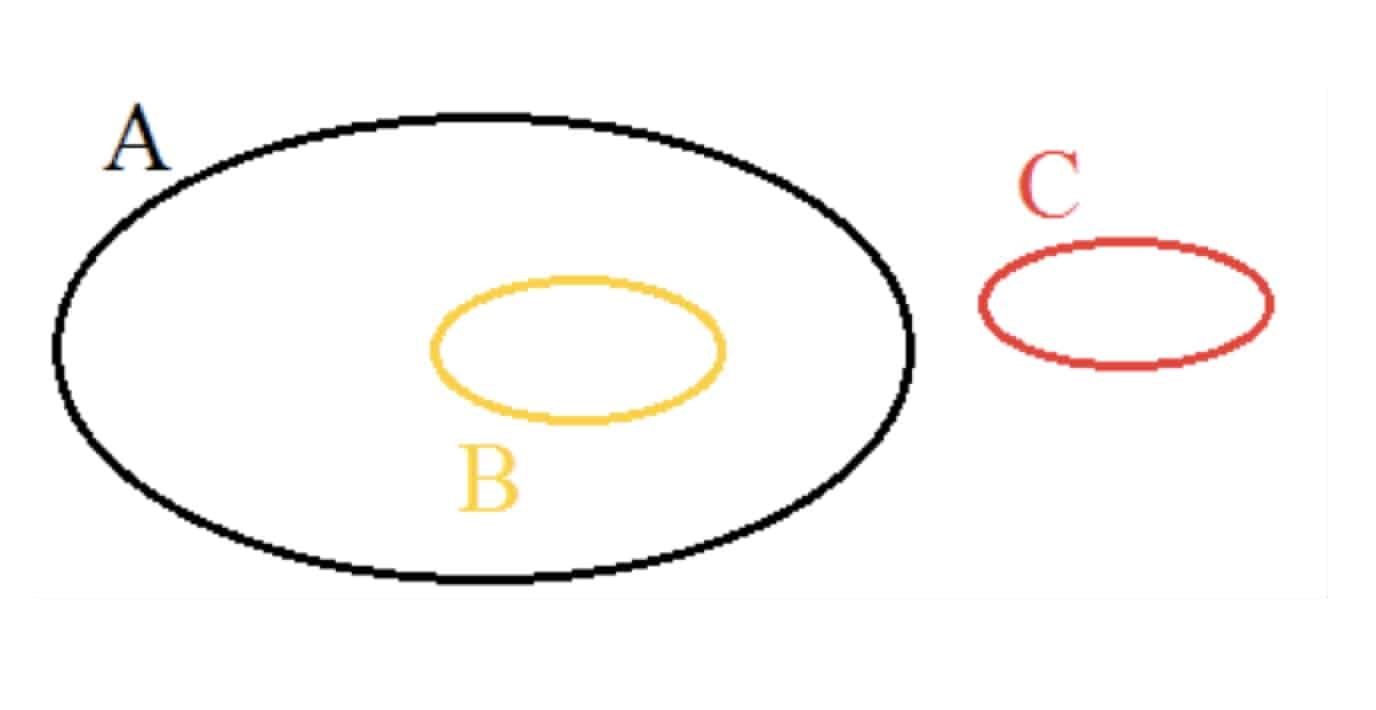
Donc si vous tirez un échantillon d’une population, vous connaîtrez cet échantillon mais vous ne saurez rien de plus sur la population, c’est-à-dire sur les éléments qui ne figurent pas dans votre échantillon. Les sondages, tels qu’ils sont pratiqués, et surtout tels qu’ils sont présentés, n’ont donc aucune valeur scientifique.

NB : Ce qui précède ne prouve pas seulement que la démarche actuelle des sondeurs est fausse. Elle explique aussi que toute action visant à obtenir une information plus large, même probabiliste, sur une population à partir d’un échantillon issu de celle-ci est vouée à l’échec.

2 – l’explication

a) la présentation la plus répandue

La première présentation que l’on trouve un peu partout comme ici (1) sur le sujet décrit la situation de la manière suivante :

(1) – https://www.cairn.info/la-methode-en-sociologie–9782707152411-page-45.htm

Illustrons-là avec un exemple. Soit une urne dans laquelle il y a des boules vertes et des boules rouges dans des proportions inconnues. On tire un échantillon de cette urne et on trouve par exemple 40% de boules vertes (donc 60% de rouges). On va estimer que la proportion de boules vertes dans l’ensemble de la population (donc de l’urne) est la même soit 40%. Cette estimation n’est qu’une supposition, rien de plus. On va ensuite calculer, dans le cadre de cette hypothèse de 40% de boules vertes dans l’urne, les probabilités d’obtenir des échantillons contenant toutes les proportions possibles et construire une courbe élégante qui résume notre travail.

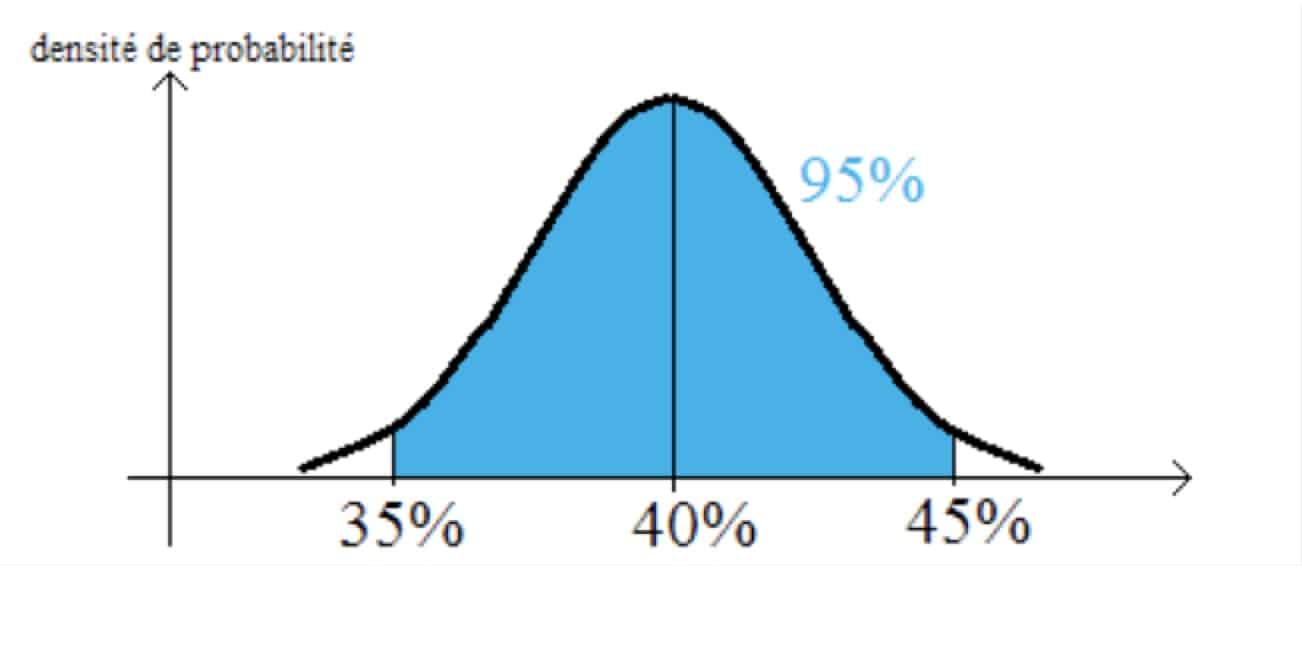
Nous constatons que nous avons 95% de chances d’obtenir dans ce cas un échantillon entre 35% et 45% de boules vertes. Et on présente ce résultat comme un intervalle de confiance sur la proportion de boules vertes dans la population. Alors que c’est en fait celui des échantillons tirés d’une population dont la proportion est connue par hypothèse. On est ainsi passé de :

j’ai une urne avec 40% de boules vertes

=>

j’ai 95% de chances d’en tirer un échantillon avec entre 35 et 45% de boules vertes.

à

j’ai un échantillon avec 40% de boules vertes

=>

j’ai 95% de chances d’avoir une population initiale dans l’urne comprise entre 35% et 45% de boules vertes.

C’est un enchaînement absolument injustifié un peu comme un tour de passe-passe. Voir cet exemple pas spécialement choisi (2) tant ils sont nombreux. Il est vrai que dans un texte émanant d’une autorité (un enseignant en qui on fait confiance), écrit dans un langage un peu technique (avec les symboles mathématiques adéquats), où l’on va évoquer des notions nouvelles comme celle d’estimateur puis la question de savoir si un tel estimateur peut-être biaisé et comment il peut l’être, etc. etc. il est facile de tromper son monde à commencer par l’auteur du document lui-même. Dans l’article cité, il est même renvoyé en annexe une partie de la démonstration !

(2) – https://lrouviere.github.io/doc_cours/poly_sondage.pdf

Il faut toutefois admettre que dans la très grande majorité des cas, ces présentations sont l’œuvre de personnes qui ne sont pas des mathématiciens. Ce sont pour la plupart des enseignants mais dans des matières autres telles que la biologie, les sciences humaines, etc. Et la très grande majorité des auteurs le reconnaissent très honnêtement

« L’enseignement des statistiques est donc étranger à ma pratique professionnelle habituelle. J’y suis venue en raison des besoins propres à la licence Sciences et Humanités. En effet, l’emploi des statistiques est aujourd’hui inévitable dans de nombreuses branches de la biologie ou des sciences humaines qui figurent au programme d’enseignement de la licence. »

(3) – https://books.openedition.org/pup/42920?lang=fr

b) la vision des mathématiciens

Les statisticiens formés aux mathématiques ne sont certainement pas dupes sur ce qui précède mais semblent laisser faire. Pourquoi admettons-nous ici qu’ils ne sont pas dupes ? Tout simplement parce qu’ils ont bien tenté de contourner cette difficulté logique que nous avons évoquée dans notre démonstration. Ils en sont donc conscients. C’est ici qu’intervient ce qu’ils appellent « inférence ». L’inférence est donc un essai de remonter à la population à partir d’un échantillon. La plus belle réussite en la matière (devrions-nous dire la seule ?) est celle de Thomas Bays. Précisons que cette inférence n’utilise pas les probabilités en sens inverse du sens logique mais qu’elle « remonte » à une autre population : une population de populations.

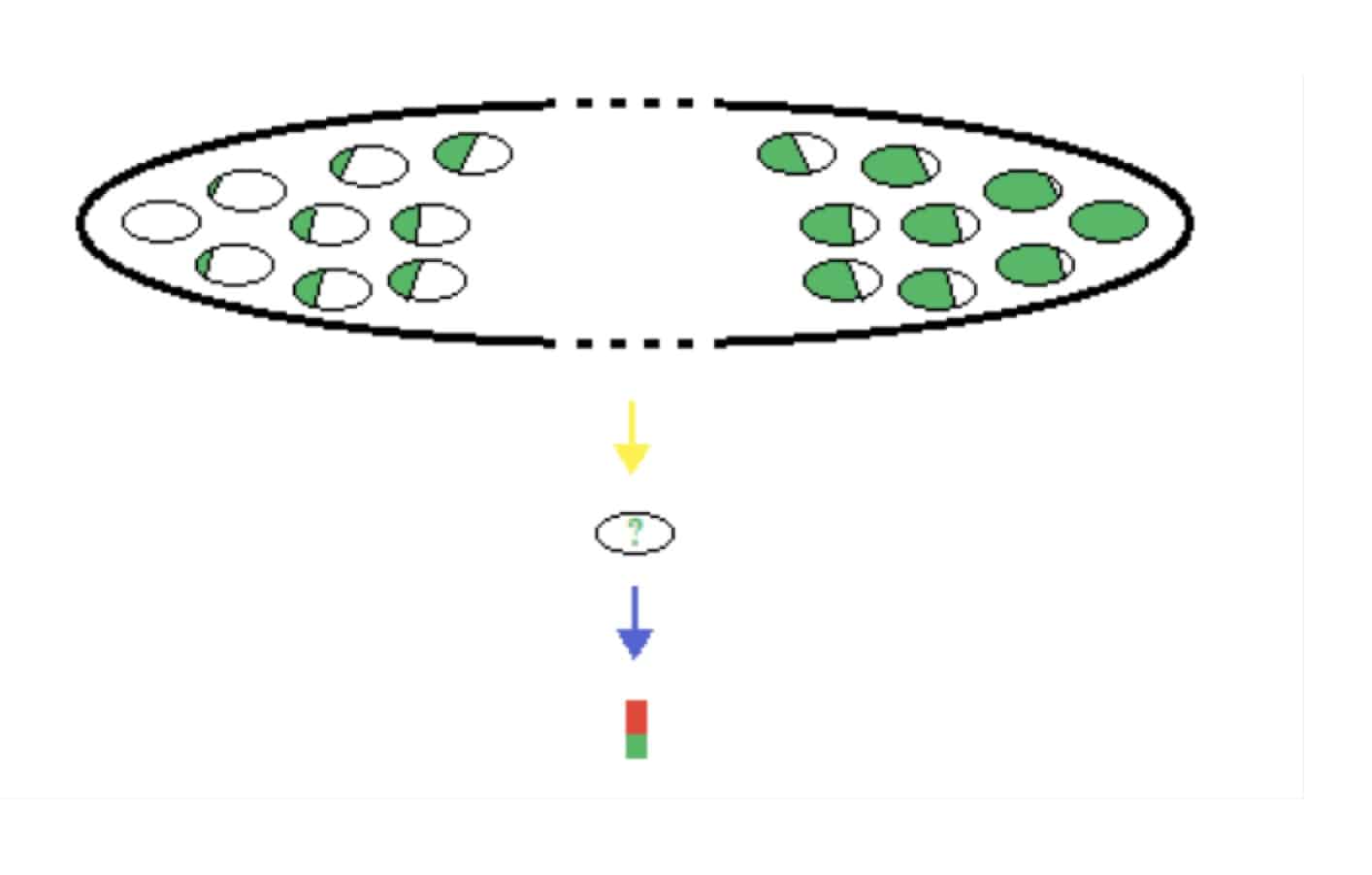
Dans ce schéma, on considère la population de toutes les urnes possibles. La providence en a tiré une (au hasard ?). C’est la flèche jaune. Ce tirage, dans lequel nous n’avons aucune part, nous a donné notre urne dont nous ne connaissons pas le contenu exact. Puis, nous tirons un échantillon de celle-ci, c’est la flèche bleue. L’inférence bayesienne fait bien le calcul dans le bon sens c’est-à-dire de la population vers l’échantillon : ici du haut vers le bas.

La démarche consiste à prendre en compte toutes les populations possibles, à calculer dans chacune d’elles la probabilité d’obtenir l’échantillon tiré de la population initiale et de réduire donc l’univers des possibles à ceux qui donnent cet échantillon.

Dans le cas de notre urne, cela revient à considérer toutes les proportions possibles de boules vertes autrement dit de 0 à 100%, puis de calculer, pour chacune de ces populations, la probabilité d’obtenir un échantillon avec 40% de boules vertes (on peut déjà comprendre que la population qui contient 0% de boules vertes a une probabilité nulle de fournir l’échantillon que nous avons avec 40% de boules vertes).

Et force est de constater que la courbe obtenue est très proche de celle utilisée par les non-spécialistes. Les différences existent mais peuvent ici être négligées.

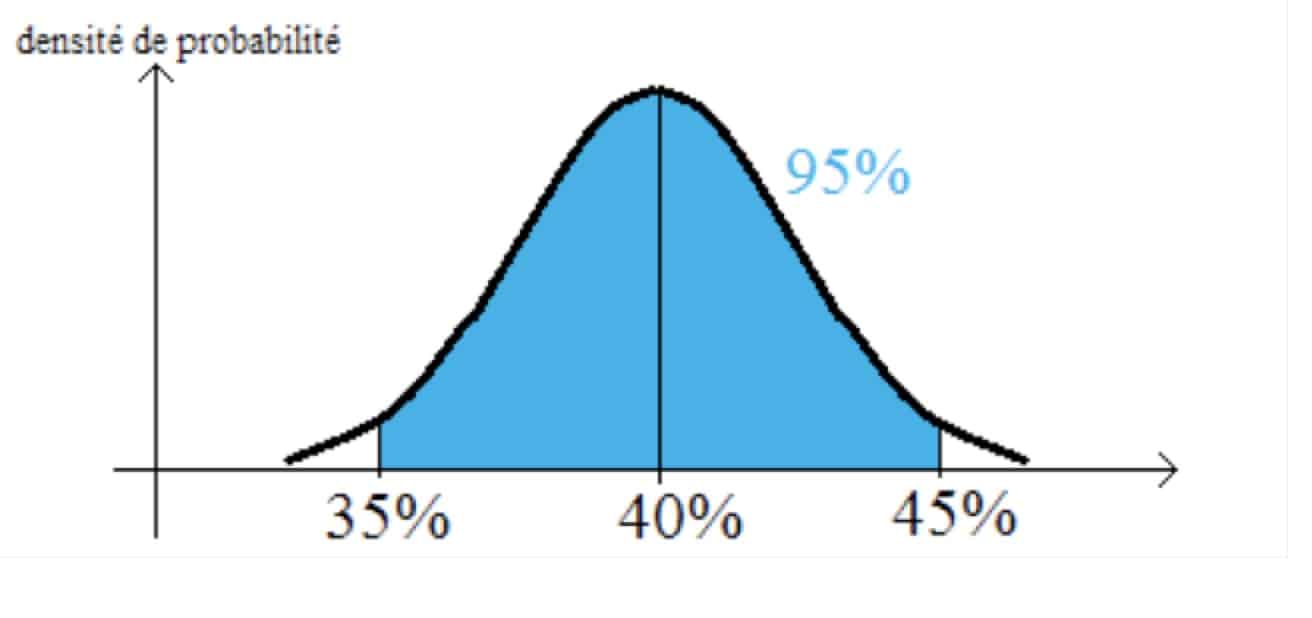
Cette fois, la figure ne présente pas en abscisse les échantillons mais les populations, chacune avec sa proportion de boules vertes. Les probabilités sont celles de donner l’échantillon que nous avons, donc celui avec 40% de boules vertes. On ne s’étonnera pas de constater que ce sont les populations avec des proportions voisines de celle de notre échantillon qui ont le plus de chances de le donner.

L’inférence bayesienne consiste maintenant à calculer un intervalle de confiance qui va, comme la figure elle-même, être très proche des résultats des sondeurs non mathématiciens.

C’est d’ailleurs une inférence bayesienne qui a été utilisée par le laboratoire Pfizer pour l’évaluation de son vaccin anti-covid Comirnaty par les instances européennes chargées de lui accorder ou non une autorisation de mise sur le marché (4).

(4) https://www.ema.europa.eu/en/documents/assessment-report/comirnaty-epar-public-assessment-report_en.pdf (page 80)

Cela semble maintenant justifier la pratique des sondeurs.

Sauf que non.

En effet, la figure ci-dessus n’est utilisable telle qu’elle qu’en supposant que toutes les populations sont équiprobables. Autrement dit, il faut faire l’hypothèse qu’il est tout aussi probable d’avoir une urne avec 40% de boules vertes qu’une autre avec 0%. Pour un sondage électoral, cela correspondrait à considérer qu’il y a autant de chances que personne ne vote pour tel candidat, que 5% ou 10% votent pour lui, ou 20% etc. Ce qui n’est manifestement pas le cas. Prenez n’importe quelle situation électorale, avant le scrutin, et il vous apparaîtra évident que pour un candidat donné les scores compris entre 0 et 100% ne sont pas équiprobables.

Les statisticiens de Pfizer le savent parfaitement puisqu’ils ont considéré une répartition de probabilité qui n’est pas l’équiprobabilité au moment d’effectuer leurs calculs. Ils ont donc bien utilisé cette inférence et non pratiqué comme la plupart des non-mathématiciens comme nous l’avons décrit précédemment.

Il est en effet nécessaire, insistons, indispensable, d’effectuer une hypothèse initiale sur la répartition en probabilités de ces populations « possibles ». Et bien entendu, il faut justifier de cette hypothèse. Si celle-ci est certaine, alors ce n’est plus une hypothèse, et les résultats obtenus ne seraient pas soumis à la critique présente. Il en resterait quand même une autre, et non des moindres, que le tirage soit bien effectué au hasard. Et il faut bien comprendre que nous ne parlons pas ici du tirage de l’échantillon par les expérimentateurs mais du tirage « au hasard » par la nature, un Dieu, ou quoi que ce soit d’autre, d’une population parmi l’ensemble des populations possibles.

Quand les sondeurs ne présentent pas cette hypothèse de répartition des populations (et le plus souvent ils n’en parlent même pas) alors ils privent leurs calculs de toute base scientifique. Et donc leurs résultats aussi.

Quand les sondeurs considèrent une hypothèse donnée, alors il faut comprendre que les résultats ne sont valides que sous réserve de la validité de cette hypothèse. Quand celle-ci n’est pas chiffrée, que valent les 95% de l’intervalle de confiance ? Que vaudrait une réduction de 95% obtenue dans un magasin sur un tarif inconnu ? C’est en étant conscient de cela que le laboratoire Pfizer a présenté une hypothèse chiffrée. Rien qu’à ce stade, on note le décalage entre les mathématiciens (ici, ceux d’un laboratoire pharmaceutique privé) et les utilisateurs venus d’autres horizons tant publics que privés, chercheurs, enseignants ou techniciens instituts de sondage.

Quand cette hypothèse est chiffrée mais pas justifiée, c’est-à-dire qu’il n’est présenté aucune raison valable de considérer cette hypothèse plutôt qu’une autre, la justification scientifique n’est plus valable. C’est malheureusement le cas du laboratoire Pfizer qui a ainsi privé de toute justification scientifique l’efficacité du vaccin Comirnaty annoncée à 95% (5).

(5) – https://ordus.fr/documentsPDF/Non95.pdf

Même si cela est difficile à croire, nous exposons bien ici le fait que la pratique des sondages est complètement dépourvue de justification probabiliste. Et pourtant, il est souligné lourdement un peu partout l’importance des mathématiques, et plus spécialement des probabilités, dans l’ensemble des autres sciences et on peut y inclure la physique. Voici un exemple particulièrement illustratif :

« La théorie mathématique des probabilités fait aujourd’hui partie intégrante des sciences exactes, et son importance intellectuelle et pratique dépasse de loin les simples jeux d’argent. »

(6) – https://www.agrobiosciences.org/IMG/pdf/sondages_probabilites.pdf

3 – Pourquoi

Alors comment en est-on arrivé là ? Ici, pas de démonstration mais une réflexion pour tenter de comprendre en ébauchant des hypothèses dont chacun se fera son idée… ou décidera de la soumettre à un examen scientifique. Dans ce dernier cas, nous recommandons vivement au préalable la lecture de ce document (7).

(7) – https://ordus.fr/documentsPDF/tests%20statistiques.pdf

La plupart des sciences, particulièrement les sciences sociales mais aussi la psychologie et même la biologie, souffrent de ne pas être reconnues au même titre que les mathématiques ou éventuellement la physique. Avec l’arrivée des probabilités, il a semblé possible d’utiliser cet outil pour donner une couche de légitimité aux résultats de ces sciences. Aujourd’hui encore, la médecine balance entre science et art. La confusion qui existe, et pas seulement au sein du grand public, entre biologie et médecine fait que cette hésitation touche aussi la biologie. Bien entendu, ceux qui séparent biologie et médecine ne sont pas concernés. Mais rappelez-vous le nombre de médecins de plateau au moment de la crise covid et la qualification de leur propos par les journalistes en tant que « discours scientifique ».

Le besoin de reconnaissance des sciences sociales est encore plus important que celui de la biologie.

Curieusement, c’est pourtant des sciences sociales que viendront les premières remises en cause (8) .

(8) – https://www.cairn.info/revue-management-2010-2-page-100.htm

Mais la démarche restera à l’état d’ébauche. Il est difficile de poursuivre des travaux quand les résultats obtenus mettent à bas une partie du savoir des scientifiques connus et reconnus, des professeurs qui ont enseigné pendant des années une démarche erronée.

(Ici un article publié dans Pour la Science, une revue de vulgarisation très sérieuse qui reprend en général les publications de Scientific American :

https://www.pourlascience.fr/sd/mathematiques/peut-on-croire-aux-sondages-3036.php

Ce texte ne porte que sur les biais connus, laissant entendre que le reste de la pratique des sondeurs est valide. Et son auteur est un homme brillant et reconnu :

https://www.sfds.asso.fr/fr/origines_et_fonctionnement/680-hommages/

Quelle serait la crédibilité d’un exposé comme le nôtre qui met à bas tout cet édifice ?

Comment questionner l’enseignement d’universités prestigieuses ?

http://www-irem.univ-paris13.fr/site_spip/IMG/pdf/Brochure118_StatInf.pdf

Surtout que le problème n’est pas français mais mondial : https://unesdoc.unesco.org/ark:/48223/pf0000059785_fre

Comment remettre en cause l’utilisation des mathématiques à l’appui des sondages quand celle-ci est validée y compris par ceux qui voudraient attaquer les sondages comme cette publication d’un mouvement politique : https://www.gauchemip.org/spip.php?article1798

L’histoire des sciences est pleine de ces exemples où il a fallu attendre que de nouvelles têtes émergent, qu’une génération remplace la précédente pour enfin surmonter ces blocages. Il existe des cas célèbres comme celui d’Eugène Parker, ridiculisé quand il a développé la théorie des vents solaires puis réhabilité au point de voir la sonde de la NASA lancée en 2018 vers le soleil baptisée avec son nom. D’autres sont moins connus comme le « télémobiloscope » inventé en 1904 par Christian Hülsmeyer qui n’intéressa personne alors qu’il s’agit rien de moins que du premier radar (https://fr.wikipedia.org/wiki/Christian_H%C3%BClsmeyer) ! Ou encore celui du pourtant déjà connu et reconnu inventeur de la machine à vapeur, James Watt, qui en 1873 se serait, selon certaines sources, couvert de ridicule en avançant devant la Société Royale de Londres que l’hydrogène pouvait brûler pour donner de l’eau ! (https://www.jstor.org/stable/41821378)

Dans ces exemples, la réalité a fini par s’imposer et mettre à bas les réalités subjectives des êtres humains. Pourquoi cela ne s’est-il donc pas produit pour les sondages ?

La réponse pourrait tenir à deux choses. D’abord qu’il est fréquent que les sondages ne s’écartent pas trop de la réalité. Il est rare qu’un candidat ayant été élu au premier tour des élections ait été crédité d’un score si nul par les sondages qu’il n’était supposé ne même pas franchir ce premier tour. Ensuite, quand cela arrive, il suffit de se rappeler la nature probabiliste de la démarche et de penser qu’il est normal que quelquefois la réalité tombe hors de l’intervalle de confiance. Et si ces écarts sont trop nombreux pour que cette dernière explication soit crédible, alors il suffit d’incriminer d’autres biais des sondages. Dans tous ces cas de figure, la justification des mathématiques est épargnée. C’est d’ailleurs flagrant dans l’exemple que nous avons cité:

« Mais d’abord est-ce qu’on peut avoir confiance aux résultats des sondages publiés ?

La réponse est « oui , mais », et la preuve est fournie scientifiquement par la loi des grands nombres. (****) »

https://www.gauchemip.org/spip.php?article1798

NDLA : Les astérisques entre parenthèses renvoient simplement à un article de wikipedia sur la théorie des grands nombres sans plus d’analyse.

Toutes ces considérations sont des pistes sérieuses permettant de comprendre que la réalité n’ait pas pu s’imposer à des êtres humains tellement désireux de maîtriser le hasard qu’ils en devenaient aveugles. Mais il peut y en avoir d’autres.

Le plus frappant, dans le cas des sondages, c’est que tout ce qui précède est compréhensible par tout le monde à condition d’être attentif, et notamment par un lycéen en terminale scientifique. Ceux-ci sont pourtant nombreux chaque année à étudier les probabilités. Aucun n’a poussé la réflexion sur ce qui leur est enseigné ?

Il serait intéressant de voir comment serait noté une réponse à un sujet du baccalauréat portant sur un sondage qui reprendrait ce que nous venons de présenter. Comme celui-ci : terminale ES 2017

http://yallouz.arie.free.fr/bacannales/2017-France_R/2017-France_R.php?page=exo1c

Pour ceux qui le désirent, une étude complète du sujet que nous venons de traiter a été publiée ici: https://ordus.fr/documentsPDF/sondages.pdf

Didier Suardi et Quentin Vallad

Crédit photo : DR
[cc] Breizh-info.com, 2022, dépêches libres de copie et de diffusion sous réserve de mention et de lien vers la source d’origine